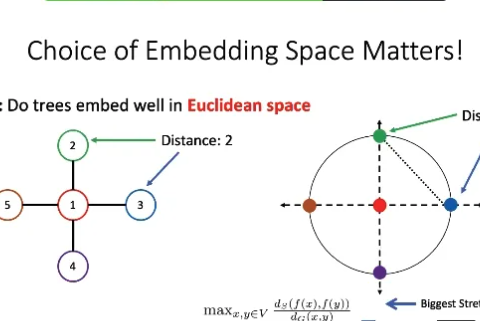
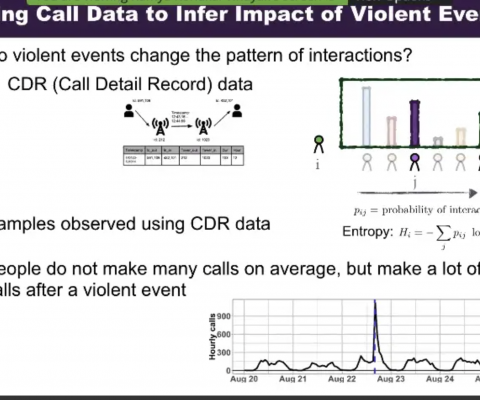
Welcome to the Systems, Information, Learning and Optimization (SILO) research group at the University of Wisconsin-Madison. SILO aims to build a community of mathematically-minded researchers interested in computational and mathematical sciences.
SILO is about breaking down the “silos” of research created by academic department boundaries. Recent advances in information science are allowing scientists and researchers to sense, process and share data in ways and scales previously impossible. These developments have the potential to benefit work happening in a wide range of disciplines. SILO’s purpose is to help realize such potential by providing the time and space for researchers to present and interact to find common threads.
The weekly SILO Seminar Series is made possible through the generous support of American Family Insurance.

We will be holding hybrid seminars, with both in-person and virtual (Zoom) participation. Pizza will be served for the in-person attendees. Please join the SILO mailing list for an RSVP link for in-person seminar attendance or Zoom information ahead of each seminar.